Physicists create world’s most ‘fiendishly’ difficult maze

In a paper recently published in the journal Physical Review X, three British physicists describe how they produced what they call a . “the most devilishly difficult maze ever created”.

By combining the principles of fractal geometry with the infinite repetition of a basic pattern and the ancient move of the knight in the game of chess, they came up with a result. So-called Hamiltonian cycles are defined in graph theory as paths that visit each vertex once and return to the initial vertex, forming a closed loop..

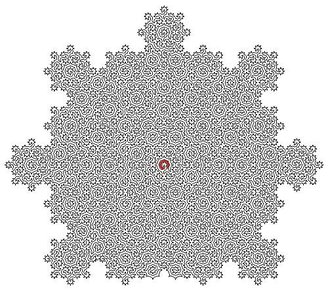
This pattern, known as Ammann-Beenker tiling in flat coatings, creates complex fractal labyrinths representing quasicrystals. These solid structures are likened by the authors to an exotic form of matter because of their unique physical and structural properties that distinguish them from traditional crystals.

Mazes built by “horse walking”

The team used the “L” displacement of the knight in the game of chess, a common move, to generate an infinite number of Newtonian loops. These loops get bigger and bigger until they describe exotic matter called quasicrystals.Found only in nature on a Siberian meteorite, this shape slices through living crystals in six dimensions.

The fractals formed by the quasicrystals are described in a press release as “an atomically sharpened pencil”“ drawing straight lines around all neighboring atoms, connecting them without lifting the tool from the paper and writing over the lines.

Replacing the pen with an atomically sharp microscope tip that produces images of individual atoms, These Hamiltonian loops will create the easiest paths to the electronic deviceThis will be very useful in research, as the process, known as scanning tunneling microscopy, can take up to a month to complete.

Harder than the Minotaur’s Labyrinth?

To get an idea of ​​the complexity of the labyrinths developed in this research, it is useful to make a comparison with the legendary Minotaur labyrinth designed by Daedalus in Greek mythology. This trap, designed to punish young Greeks, It was a physical and mental challenge that also trapped the beast..

Although thought to be impassable, the Minotaur’s labyrinth was a finite and concrete structure, with a clear entrance and exit. The goal here was to find a way to escape. So, although it was complex, it did not require advanced mathematical tools.

Ammann-Beenker labyrinths are based on quasi-periodic models that display advanced mathematical and structural complexity. Characterized by aperiodic and unusual symmetries, They depend on determining the Hamiltonian cycles to be solved mathematically..

Possible practical applications of the impassable labyrinth

These unique labyrinthine creations are not only aimed at solving aesthetic problems, but also have potential uses in various scientific and technological fields. By exploring the complexity and properties of Hamiltonian cycles, this work helps solve some difficult problemsFrom finding faster routes for vehicles to understanding protein folding.

Research has also shown that quasicrystals can be made into highly functional adsorbents. Adsorption, a process in which molecules stick to the surface of a solid, can be used to capture carbon to prevent the gas from entering the Earth’s atmosphere.

Efficient adsorption could make quasicrystals very useful catalysts for reducing the energy of chemical reactions and increasing industrial efficiency, explains research leader Felix Flicker from the University of Bristol in the United Kingdom in a statement. “So in this scenario, we make some seemingly impossible problems treatable,” he concludes.

Do you have any questions? Tell us about it on our social networks and understand once and for all why learning exact sciences is so difficult. Until later!